 It is always good to get the chance to actually teach real kids in a real school. I have always said that if you are going to teach students about linear functions, it would be a crime to do it without any technology. So, up comes the topic and in I go with the technology. We have organised a class set of HP Prime handhelds for the school and my job was to get students started using them, so they would be sufficiently familiar at the start of the linear functions topic. Continue reading Technology and Maths Exploration
It is always good to get the chance to actually teach real kids in a real school. I have always said that if you are going to teach students about linear functions, it would be a crime to do it without any technology. So, up comes the topic and in I go with the technology. We have organised a class set of HP Prime handhelds for the school and my job was to get students started using them, so they would be sufficiently familiar at the start of the linear functions topic. Continue reading Technology and Maths Exploration
Tag Archives: Graphing Calculator
HP Prime Instant Set Up and Update
I had the opportunity to visit the very beautiful Swiss city of Zurich last week to run a session for Swiss senior high school maths teachers. It is always very interesting to see the differences in the way that mathematics teaching and indeed schools are in different countries. Firstly, the school is for ages 16-19 and has roughly 3000 students in a city centre environment. Striking interior architecture, excellent catering facilities, a range of fascinating teaching spaces and a very well equipped presentation room were all very impressive (and that’s not to mention the three floors of underground heated car parking!) Continue reading HP Prime Instant Set Up and Update
Talking Maths in the Esoteric Domain: HP Prime Wireless
At the ATM London Branch conference on Saturday, Kate Gladstone-Smith from Langdon Park School in East London, presented her research into the nature of communication she had observed in maths classrooms and how this differed according to the set, the students were in. (Anyone not from the UK will need to know that in English schools teachers decide in advance how well students will do with a subject and place them in ‘top’ and ‘bottom’ sets (i.e. class/teacher groups) accordingly). Continue reading Talking Maths in the Esoteric Domain: HP Prime Wireless
Wireless Prime has arrived!
I took delivery of a box of new Primes with the wireless kit last week. This is really exciting. From a pedagogic point of view, it seems to me that the big move is to generate genuine classroom dialogue, supported by serious technology. The Prime solution gives you enough machines for a class, in a box you can easily hold in one hand. You give them out to your students. They turn them on. You launch the connectivity software on your PC and that’s it. Everyone is connected. Continue reading Wireless Prime has arrived!
Pinch to Zoom on the HP Prime!
If you have an HP Prime (if you haven’t then naturally, you must get one!), plug it into your computer via USB, launch the connectivity kit and prepare to be amazed by the smoothest upgrade you’ve ever seen! On launching, the connectivity kit asks if you want to upgrade the kit and the calculator. You certainly want to do both. When the connectivity kit is finished, launch it again and turn the calculator on. You will be promPted to continue, but aside from that it will get on AND update the calculator’s firmware. Total about 3 minutes, with the the calculator part taking a minute or so. Continue reading Pinch to Zoom on the HP Prime!
IT supporting kids learning in maths: what is the problem?
I completed my PGCE in 1983 (oh my!) and went to work in a comprehensive school in Corby new town in the East Midlands. (Then it was the largest town in England without a railway station, somewhat depressed by the closure of the largest steelworks in Europe). The walls of my classroom had a large bench running all the way round. On this bench were set out about 8 RM 480Z work stations. For anyone who doesn’t remember, these were competitors to the BBC Micro. When I taught transformational geometry, I could pause in the lesson and get my students to gather round the computers and engage with an activity I set up for them where they would create a shape and transform it using LOGO. They would make hypotheses and test them, seeing the result immediately, visually, dynamically.
I have recently observed a number of lessons on transformational geometry in London comprehensives. Despite every classroom being fully equipped with a networked computer and an interactive whiteboard and in every case, the teacher having been trained within the last year on using GeoGebra to teach transformational geometry, not one single diagram moved at all in any of the lessons. Students were shown object and image and asked what transformation connected them. An agreement was reached (often with much disagreement and uncertainty) and that would be that. There was no way that anyone could validate the agreement or see the transformation enacted. This is the traditional teaching method of ‘proof by teacher says’ or its slightly more inclusive counterpart ‘proof by agreement’. Now, just in case anyone who was there in the room with me can recognise themselves, I should share that everything else about all of those lessons was really good, sometimes quite outstanding. It is simply that giving kids experience of the mathematics, rather than showing them how it works, seems to be such a long way from conventional school practice, that even with everything else in place, teachers find it hard to achieve. Yet in 1983, it was just what you did and we had reliable technological tools ready in the classroom to support it.
I have had lengthy discussions about technology in the classroom with colleagues in teacher education and most recently I have heard about the various classroom manager systems that are being developed by the hardware companies and the IWB people. The essential premise is that you connect to handheld devices that the students have. The screens of their devices are available in thumbnail format on the teacher machine and hence the classroom screen (and able to be enlarged to show the whole class the work of an individual). The software has polling and analysis, so questions and messages can be sent and answers received and engaged with. With this level of technology available, it will again be possible to do what I was happily doing in 1983, interrupting an ordinary lesson in an ordinary classroom to engage with an idea dynamically using technology and seeing what the students are doing (I wandered round and looked at the screens and if I saw something interesting, I got the others to come over and see). At the moment, teachers feel they have to book the computer room to achieve this effect and we all know how unlikely/impossible that is.
But it is a compelling thought. Now, the teacher can manage the dialogue, setting a task, students can engage with the software and discuss the issues. When ideas emerge these can be shared with the whole class. A real dialogic engagement. So, what’s stopping us? Wheel the trolley of laptops in and they will connect seemlessly to the network with no fuss and then it’s OK? Of, course it doesn’t/won’t. Not least because controlling dynamic software from a track pad is a nightmare, but have you ever made a half class set of Laptops connect to a network? So, bring in the set of iPads the school just massively invested in. Agh. No manager software and as yet only a very cut down version of GeoGebra.
The Holy Grail is that everyone turns their smart phones on and launches the iOS or Android app they need, and we get some generic tablets for those that don’t have smart phones and these all connect. Even then we would need better software (unless you invest £30 a head for TI-nspire on iOS which is really good). I hope to get delivery of a trial set of HP Prime wireless graphing calculators very soon. Naturally, they do everything that that I have said. The massive difference is that they have an auto detecting dongle (the same as the ones that make wireless keyboards work). No installation, no logging in, if the device is in the room, the screen appears on the teacher machine. People say: ‘what’s the point of graphing calculators these days?’ I say: it is a piece of bespoke hardware with an optimised interface for the range of maths functions you need, with really well developed and well thought out maths software. Moreover, compared to iPads they are really cheap. They are small, easy to carry and importantly easy to charge. You just have to be able to grab the box on your way into lesson and hand them out the same as you would hand out rulers and compasses and they just work when you turn them on. Only then can we get back to 1983 and have technology seemlessly integrated into ordinary lessons in ordinary classrooms. Only now we’ve got rather classier software to play with.
I would like to work with anyone who is using any comparable kit that can achieve the same effect. I would be delighted to set up a research project where we can examine the actual classroom use of these technologies. I would be keen to hear from schools who think that this sort of kit will solve the problem of static teaching and would think they could use such technology all the time (not just special occasions). I would happily support such work with loan equipment and support materials. Contact me (chris@themathszone.co.uk).
Apart from the dodgy hairdos and the rusty cars, 1983 had things going for it!
Update for HP Prime
Calling all HP Prime owners. Make sure your ROM is up-to-date. The latest update was released early in December. A quick check is to see if you have the full calender function which is new in this release. (Tap in the top write corner to show the setting, then tap on the date. A full calender will come up if you have the new version, if not, go update!). The procedure is unbelievably simple.
You need the connectivity kit installed on a PC and your HP Prime ready to connect with a USB cable. (The connectivity kit software is on the CD or available to download on my web site. Click here). Run the software. It will probably prompt you to update it when launched. Do this and follow the prompts to complete the installation. When complete, launch the software again and plug the calculator in with your USB cable. You will see the your calculator listed. Right click on the name HP Prime and choose update firmware. Follow the prompts. That’s it. Your Prime should be ready. Double check by marveling in the new Calender facility. Check here for a video showing the checks.
The HP community is in full swing now, check out these videos for HP Prime games by the wonderful MicNic Tetris and ‘Angry Birds‘ and MasterMind from Tony Galton.
Classroom Maths Dialogue with a Handheld
Now that HP prime is launched and I have a few of them to play with (oh and to run training sessions with …) the implications can be tested of having handheld maths technology that connects easily to the teacher computer in a classroom. Ultimately the connection will be wireless but the dongles will not be available until early next year. So, I bought some 5m micro USB cables and could test it in teaching situations. So far only teacher groups, but I’m getting the hang of it.
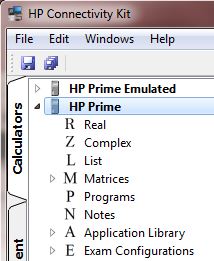 There is free emulator software and the connectivity kit is freely available too. You can try this out yourself by opening a number of instances of the emulator and the connectivity kit on your PC. Just go to http://www.hpgraphingcalc.org/hp-prime-links-and-resources.html for the files. The most impressive thing is how utterly seemless it is. Install the connectivity kit and launch the software. Down the side there are three tabs: ‘Calculators’, ‘Content’ and ‘Class’. Just plug in an HP Prime calculator (or launch an instance of the emulator software and you will see it listed. Here, I’ve plugged in one real machine and am running my emulator. Clicking next to the device brings down a view of all of the content on the machine. Clicking the content tab allows us to author new content and then save it to the machine. You can create tests and polls. (Right click on the thing you want to create and ‘new’ comes up. Click that. When you are done, click the small save icon in the top left of the screen. The dialogues are pretty self-explanatory so I’ll leave you with that. When you are done, go back to the new item you created and right click to ‘send to class’ and it will be on the machine. Imagine being in a classroom in which simply by launching the software and machines being in the room, you can share content with them. No connections no log ins, just get started. But to me it bursts into life when you click the ‘class’ tab. Now you can see the screens of all of the connected machines. (Remember, when wireless is there, connected just means ‘in the same room’.).
There is free emulator software and the connectivity kit is freely available too. You can try this out yourself by opening a number of instances of the emulator and the connectivity kit on your PC. Just go to http://www.hpgraphingcalc.org/hp-prime-links-and-resources.html for the files. The most impressive thing is how utterly seemless it is. Install the connectivity kit and launch the software. Down the side there are three tabs: ‘Calculators’, ‘Content’ and ‘Class’. Just plug in an HP Prime calculator (or launch an instance of the emulator software and you will see it listed. Here, I’ve plugged in one real machine and am running my emulator. Clicking next to the device brings down a view of all of the content on the machine. Clicking the content tab allows us to author new content and then save it to the machine. You can create tests and polls. (Right click on the thing you want to create and ‘new’ comes up. Click that. When you are done, click the small save icon in the top left of the screen. The dialogues are pretty self-explanatory so I’ll leave you with that. When you are done, go back to the new item you created and right click to ‘send to class’ and it will be on the machine. Imagine being in a classroom in which simply by launching the software and machines being in the room, you can share content with them. No connections no log ins, just get started. But to me it bursts into life when you click the ‘class’ tab. Now you can see the screens of all of the connected machines. (Remember, when wireless is there, connected just means ‘in the same room’.). 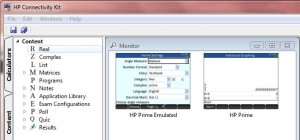 These refresh every couple of seconds (although right click and refresh speeds this up if needs be. Also, right click and ‘project’ creates a resizeable image to show the whole class. So, now I can ask my class to work on a problem and watch what they do. When something interesting happens I can (if I want) bring up that screen to show the whole class. But, there is more, … I can open a messages window. From there I can send a private message to a single machine or a message to the whole class.
These refresh every couple of seconds (although right click and refresh speeds this up if needs be. Also, right click and ‘project’ creates a resizeable image to show the whole class. So, now I can ask my class to work on a problem and watch what they do. When something interesting happens I can (if I want) bring up that screen to show the whole class. But, there is more, … I can open a messages window. From there I can send a private message to a single machine or a message to the whole class. 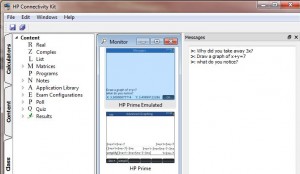 This appears on their screen and they can even respond and we can discuss. Personal in-class responses to individual students work monitoring the outcome of their thinking from the maths appearing on their screen. Now, I always say get students to work one between two, so we’ll have 15 screens up in a full classroom. I tried this with 6 Greenwich PGCE students and it is a bit frantic trying to respond individually. However, really, I should be more teacherly and give the occasional prompt looking our for the ‘Aha’ moments. The possibility to get to the nub of student understanding is tantalising. What do you think? I am dying to get the wireless dongles and try this in a routine classroom with ordinary kids. Then we’ll see what they can do. Exciting times.
This appears on their screen and they can even respond and we can discuss. Personal in-class responses to individual students work monitoring the outcome of their thinking from the maths appearing on their screen. Now, I always say get students to work one between two, so we’ll have 15 screens up in a full classroom. I tried this with 6 Greenwich PGCE students and it is a bit frantic trying to respond individually. However, really, I should be more teacherly and give the occasional prompt looking our for the ‘Aha’ moments. The possibility to get to the nub of student understanding is tantalising. What do you think? I am dying to get the wireless dongles and try this in a routine classroom with ordinary kids. Then we’ll see what they can do. Exciting times.
What is this maths that we are teaching?
It is with envy that some mathematics educators in England look to our colleagues in the Netherlands where the Freudenthal institute has generated a rich, coherent research debate which has been widely implemented in schools. Realistic Mathematics Education offered the antidote to the formalism of the New Maths based on Hans Freudethal’s view that mathematics was not pre-formed. He said; “… the global structure of mathematics to be taught should be understood: it is not a rigid skeleton, but it rises and perishes with the mathematics that develops in the learning process. Is it not the same with the adult mathematician’s mathematics?” So it is very sad to hear that the Commission for Examinations in the Netherlands is considering banning graphing calculators from public examinations. What is it that a calculator does that could be damaging to mathematics developing in the learning process? A machine can do only what a machine can do. If mathematicians continue to fulfill an important role, then clearly they must be able to things that machines cannot do. In his 2001 novel, Uncle Petros and Goldbach’s Conjecture, Doxiadis’ eponymous mathematician dismisses any process a machine could do as ‘shopping maths’. That of course includes anything a computer algebra system (CAS) could do.
So, learners of Freudenthal’s mathematics should have access to the tools to do the shopping maths, to free up the thinking space to engage with real mathematics; solving problems, generating conjectures, developing proof. These are the art of mathematics, not the mechanical grind. Godfrey Hardy acted as the foil to Ramanujan’s genius, but in the ‘apology’ he makes clear how well he understood that Ramajan’s ability for finding extraordinary new relationships that only he could see, was the real mathematical gift. Getting it into a publishable state was the routine work for afterwards.
The excellent Project Euler takes as it’s premise that mathematicians will have access to a high level programming language (Python, which naturally has a powerful CAS) to engage with problems in number theory. The wonderfully named https://brilliant.org/ designed for potential International Maths Olympiad candidates has a whole section of problem solving requiring programming (and hence CAS) available.
Having a machine capable of high level mathematics available in a public examination in mathematics forces examiners to take a considered view of what the maths is that they are examining. It prevents them from asking students to replicate what machines can do and focuses their thinking on the maths that matters. The maths that Hans Freudenthal was so keen to preserve in the Netherlands, against the onslaught of formalism.
This sad situation was brought to my attention through the English translation of a response by Erik Korthof to an advert for the new HP Prime graphing calculator. He suggests that the absence of graphing calculators in the past allowed the construction of ‘proper exams’. The task of mathematics education should not be to make the lives of examiners easy. Clearly, asking a student to complete a mechanical task that would be simply done by a machine is very simple. To construct a question knowing that the student has access to such a machine is hard. Specifically so, because the question must demand genuine mathematical thinking and that puts great demands on examiners. In the UK, the most progressive mathematics education project (MEI) for A Level students (age 18) have just had their first cohort complete an examination module with a CAS calculator available. The result is thoughtful, highly mathematical questions of exactly the type University maths courses are excited to see. The link will take you to their answer to Erik Korthof’s question: “Is secondary education served with a Computer Algebra System?”. Clearly they answer a resounding yes and MEI are major players in the future of maths education in England.
As I’ve said elsewhere the existence of tools like HP Prime which allow access to powerful mathematical visualization and calculation tools in the classroom liberates students from the mechanical processes that prevent them thinking deeply about the mathematics. Certainly there will be many lessons where the calculators are put firmly away and students will learn and practice these mechanical processes, like drawing graphs and manipulating algebra, not only because they need to see how they work, but also to give them a better feel for the outcomes. Happily teachers are sophisticated enough to manage this. They can also find secure ways to use exam modes to ensure devices adhere to local regulations. Schools are expert in this. These logistical issues should not be used as an excuse for not allowing students the tools that professionals have access to and reducing what is called maths in schools to a collection of mechanical processes. Especially not from the birthplace of RME and the beautiful, powerful view of mathematics presented to the world by Hans Freudenthal.
HP Prime The New Future
 HP Prime will be launched ready for September and the new school year. Have a look at the teaser YouTube HP released to show you what it looks like. Last week I had one in my hands at a launch workshop in Prague led by GT Springer the lead designer. GT has been central to most of the major innovations in graphing calculator design and he has put all of that experience into a genuinely wonderful new device. Read the interview GT gave to the US tech blog Cemetech. First impressions matter to schools who want to show the smart new kit they are buying and to students who want something really flash in an era where new tech does indeed look good. It is interesting that after a stunned response at the NCTM conference in Colorado there has been a lot of buzz around tech sites like Slashgear and Ubergizmo. Well that’s good, because if the tech savvy think it’s worth talking about then bright young teachers and their equally bright students will take a look.
HP Prime will be launched ready for September and the new school year. Have a look at the teaser YouTube HP released to show you what it looks like. Last week I had one in my hands at a launch workshop in Prague led by GT Springer the lead designer. GT has been central to most of the major innovations in graphing calculator design and he has put all of that experience into a genuinely wonderful new device. Read the interview GT gave to the US tech blog Cemetech. First impressions matter to schools who want to show the smart new kit they are buying and to students who want something really flash in an era where new tech does indeed look good. It is interesting that after a stunned response at the NCTM conference in Colorado there has been a lot of buzz around tech sites like Slashgear and Ubergizmo. Well that’s good, because if the tech savvy think it’s worth talking about then bright young teachers and their equally bright students will take a look.
Being an old fogey myself, all I can say is that it looks very smart indeed,with a brushed aluminium front and a smooth bright screen. The colour is bright and very sharp with extremely clear detail and you just have to keep reminding your self that it is a touch screen and that you can drag and move objects and navigate drop down menus. The touch is smooth and very accurate. Younger folk than me will do this instinctively, I’m sure that they will be wondering how it could be done any other way. It is very well made and feels sleek and smooth all round. It is about 300g which feel sufficiently heavy to be solid but easy to hold and it balances really nicely in tho hands with your thumbs over the Home screen and the CAS button. You really feel you are holding a classy piece of kit. So, part one of the battle is won, savvy young people will want one and schools will be proud to show off that they bought them. So, what does it do?
The biggest headline is: wireless connectivity. Files can be transferred via the connectivity software. However, if you plug a small USB dongle (which you purchase seperately) into the top of the PRIME, it will immediately be recognised on the computer, notably the teacher’s computer in class. Files and settings can then be transferred wirelessly. (Only from PRIME to PC not from PRIME to PRIME). More than that, the PRIME screen can be shown on the teacher’s screen. Then their will be class polling functions allowing the teacher to set a question from her computer and students to offer responses from their PRIMES with the results shown in table and chart form. Just like the polling systems many schools are getting which only do this. That will be just the start of what can be done. The critical point is that this a plug-and-play system. No set up, which is a critical factor for classroom use.
The software itself initially looks like an up-rated version of the HP39gII, which it is, so you will find all of the Apps in the HP39gII working exactly the same. So, anyone who has used a HP39gII will get started immediately. However, there are three new Apps which make a big difference. There is a mathematical spreadsheet, a dynamic geometry system and the advanced grapher. Together these represent a major advance in providing an space to explore mathematical ideas. These tie together with the big pause for breath moment. The CAS button.There is no CAS/non-CAS option. A mathematical machine must speak algebra and this one does. There are two home screens; a CAS screen which deals with exact objects and the traditional home screen which deals with approximate objects. The Apps can use the last object from each of these screens and the choice is always there; CAS screen or Home screen. This recognition of the fundamental pure/applied, exact/approximate distinctions is central to an underlying philosophy which has the potential to transform the way we think about exploring mathematics. For me, this is the thing that will determine future research into maths education technology. The spreadsheet, the dynamic geometry and the advanced grapher can all take CAS and non-CAS statements and allow users to explore the results. Just to get a feeling for what this means, have a look at GT’s handouts from the NCTM conference.
Now the sad thing is that exam boards are scared of CAS and we look forward to a future where CAS systems will transform maths exams by getting beyond procedural questions and towards mathematical problem solving. Well done to MEI for getting an A-level module approved allowing CAS and look to Germany and Australia for examples where CAS is embraced. But in the UK CAS is not allowed. Well, no, CAS is not allowed in public maths exams for which any calculator IS allowed. So, it is quite clear that this machine has a CAS system, so could you use it in an exam? To be sure the answer will be yes, the machine includes a comprehensive exam mode. A menu system allows a vast range of features to be turned on or off, CAS is one of the, but suppose a particular exam disallowed solver apps, they can be turned off too. The system is password protected and the user will simply be greeted with a little round exclamation mark if they try to access or disallowed function or suppressed apps will simply be missing from the menu. For school use, the teachers sets the settings they want e.g. turn off the CAS, creates a password and then beams this setting to all of the connected PRIMES, wirelessly. A series of bright LEDS light up in the same sequence while exam mode is engaged. It is immediately clear to the exam secretary that the machine has only those facilities allowed in exams. In discussion with teachers, it became clear that this feature sets up the possibility to allow younger learners to get started with the machine in a simplified mode and actually presented exciting pedagogic possibilities too.
The exams battle is a big one and many schools still think you cannot use any graphing calculator in a maths exam, so we will need to talk with exam boards and the JCQ to make sure the message is clear enough: you can use this machine in a maths exam and without disabling it as an amazing teaching tool.
I’ve always been a fan of calculators as a learning tool. I’ve said elsewhere that tablets are exciting, but you don’t work and think like that, you need different technological tools for different functions and the resilience of the calculator as a form factor is remarkable I think for this reason. It’s a highly portable, personal thinking space. I am really excited about PRIME because it has all of the maths you could possibly want with an intuitive touch driven interface, wireless connectivity to support proper classroom dialogue in a package that everyone will want to own.
Please get in touch with me if you see the video and want to be part of early development to get really exciting maths back into our classrooms. I would be delighted to talk to you about the support I can offer.