I had the opportunity to visit the very beautiful Swiss city of Zurich last week to run a session for Swiss senior high school maths teachers. It is always very interesting to see the differences in the way that mathematics teaching and indeed schools are in different countries. Firstly, the school is for ages 16-19 and has roughly 3000 students in a city centre environment. Striking interior architecture, excellent catering facilities, a range of fascinating teaching spaces and a very well equipped presentation room were all very impressive (and that’s not to mention the three floors of underground heated car parking!) Continue reading HP Prime Instant Set Up and Update
Category Archives: Uncategorized
Talking Maths in the Esoteric Domain: HP Prime Wireless
At the ATM London Branch conference on Saturday, Kate Gladstone-Smith from Langdon Park School in East London, presented her research into the nature of communication she had observed in maths classrooms and how this differed according to the set, the students were in. (Anyone not from the UK will need to know that in English schools teachers decide in advance how well students will do with a subject and place them in ‘top’ and ‘bottom’ sets (i.e. class/teacher groups) accordingly). Continue reading Talking Maths in the Esoteric Domain: HP Prime Wireless
Wireless Prime has arrived!
I took delivery of a box of new Primes with the wireless kit last week. This is really exciting. From a pedagogic point of view, it seems to me that the big move is to generate genuine classroom dialogue, supported by serious technology. The Prime solution gives you enough machines for a class, in a box you can easily hold in one hand. You give them out to your students. They turn them on. You launch the connectivity software on your PC and that’s it. Everyone is connected. Continue reading Wireless Prime has arrived!
IT supporting kids learning in maths: what is the problem?
I completed my PGCE in 1983 (oh my!) and went to work in a comprehensive school in Corby new town in the East Midlands. (Then it was the largest town in England without a railway station, somewhat depressed by the closure of the largest steelworks in Europe). The walls of my classroom had a large bench running all the way round. On this bench were set out about 8 RM 480Z work stations. For anyone who doesn’t remember, these were competitors to the BBC Micro. When I taught transformational geometry, I could pause in the lesson and get my students to gather round the computers and engage with an activity I set up for them where they would create a shape and transform it using LOGO. They would make hypotheses and test them, seeing the result immediately, visually, dynamically.
I have recently observed a number of lessons on transformational geometry in London comprehensives. Despite every classroom being fully equipped with a networked computer and an interactive whiteboard and in every case, the teacher having been trained within the last year on using GeoGebra to teach transformational geometry, not one single diagram moved at all in any of the lessons. Students were shown object and image and asked what transformation connected them. An agreement was reached (often with much disagreement and uncertainty) and that would be that. There was no way that anyone could validate the agreement or see the transformation enacted. This is the traditional teaching method of ‘proof by teacher says’ or its slightly more inclusive counterpart ‘proof by agreement’. Now, just in case anyone who was there in the room with me can recognise themselves, I should share that everything else about all of those lessons was really good, sometimes quite outstanding. It is simply that giving kids experience of the mathematics, rather than showing them how it works, seems to be such a long way from conventional school practice, that even with everything else in place, teachers find it hard to achieve. Yet in 1983, it was just what you did and we had reliable technological tools ready in the classroom to support it.
I have had lengthy discussions about technology in the classroom with colleagues in teacher education and most recently I have heard about the various classroom manager systems that are being developed by the hardware companies and the IWB people. The essential premise is that you connect to handheld devices that the students have. The screens of their devices are available in thumbnail format on the teacher machine and hence the classroom screen (and able to be enlarged to show the whole class the work of an individual). The software has polling and analysis, so questions and messages can be sent and answers received and engaged with. With this level of technology available, it will again be possible to do what I was happily doing in 1983, interrupting an ordinary lesson in an ordinary classroom to engage with an idea dynamically using technology and seeing what the students are doing (I wandered round and looked at the screens and if I saw something interesting, I got the others to come over and see). At the moment, teachers feel they have to book the computer room to achieve this effect and we all know how unlikely/impossible that is.
But it is a compelling thought. Now, the teacher can manage the dialogue, setting a task, students can engage with the software and discuss the issues. When ideas emerge these can be shared with the whole class. A real dialogic engagement. So, what’s stopping us? Wheel the trolley of laptops in and they will connect seemlessly to the network with no fuss and then it’s OK? Of, course it doesn’t/won’t. Not least because controlling dynamic software from a track pad is a nightmare, but have you ever made a half class set of Laptops connect to a network? So, bring in the set of iPads the school just massively invested in. Agh. No manager software and as yet only a very cut down version of GeoGebra.
The Holy Grail is that everyone turns their smart phones on and launches the iOS or Android app they need, and we get some generic tablets for those that don’t have smart phones and these all connect. Even then we would need better software (unless you invest £30 a head for TI-nspire on iOS which is really good). I hope to get delivery of a trial set of HP Prime wireless graphing calculators very soon. Naturally, they do everything that that I have said. The massive difference is that they have an auto detecting dongle (the same as the ones that make wireless keyboards work). No installation, no logging in, if the device is in the room, the screen appears on the teacher machine. People say: ‘what’s the point of graphing calculators these days?’ I say: it is a piece of bespoke hardware with an optimised interface for the range of maths functions you need, with really well developed and well thought out maths software. Moreover, compared to iPads they are really cheap. They are small, easy to carry and importantly easy to charge. You just have to be able to grab the box on your way into lesson and hand them out the same as you would hand out rulers and compasses and they just work when you turn them on. Only then can we get back to 1983 and have technology seemlessly integrated into ordinary lessons in ordinary classrooms. Only now we’ve got rather classier software to play with.
I would like to work with anyone who is using any comparable kit that can achieve the same effect. I would be delighted to set up a research project where we can examine the actual classroom use of these technologies. I would be keen to hear from schools who think that this sort of kit will solve the problem of static teaching and would think they could use such technology all the time (not just special occasions). I would happily support such work with loan equipment and support materials. Contact me (chris@themathszone.co.uk).
Apart from the dodgy hairdos and the rusty cars, 1983 had things going for it!
EAL in Maths? Problem Solved!
Where we were working in South East London, a number of students would arrive in England for the first time in the middle of secondary school. They would have very little English language and would try to get into local secondary schools. The schools would turn them away because they assumed that these students would end up with poor grades and compromise their exam statistics. So, a unit was set up to support these students make the transition to school. I got together with Gwyn Jones to produce a course designed to teach the mathematics content of GCSE with the minimum of language, but developing the key technical vocabulary of maths and of school while they learnt. The materials were supported by online interactives to see the maths dynamically and practice the ideas in an open format. There was a very low language pre-test, so that the student could show what they already knew, a tracker sheet to choose the maths they now needed to work on, a large collection of activity sheets to develop the maths and a post test with the same language demands of a normal maths test to show the schools how good they were.
In the very first group of students to use the first version of materials there was a student who had just arrived from East Africa. He had been rejected by every school in the borough. He took the pre-test and got 100%. He worked on the advanced materials and did the same on the post test. He took his work as a portfolio back to the schools and immediately found a place. Within 18 months he had an A* in GCSE maths.
We are proud to announce that we have now redesigned and updated this course and made it available to schools. Called Access to Mathematics it comes as one of our course boxes (like our well known gifted and talented courses; Wondermaths and Illuminate). There is a comprehensive teacher guide with notes on running the course. Ten copies of the comprehensive student book (120 pages) and access to the online interactives, test, answers, etc. in the Access to Mathematics web site. Priced at £195 this gives access to mathematics for all of your students for whom English is an Additional Language from those who have just arrived with no English to those who appear to have conversational English, but cannot access or succeed at maths in lessons.
Everything is described diagrammatically, putting the maths into a visual structure. Two colours are used to emphasise the structure and the maths is practised through this structure, gradually peeling it away to leave the formal symbolic maths. The course worked well supervised by non-specialist teachers as it is designed largely for self-teaching. However, with access to a specialist teacher, the materials could be used for a whole range of learners where reading and language demands of any sort are an issue.
Once you have the box, further copies of the students books are available in packs of 10 priced at £45. So, you can use them as a standard class text if you want. The overall content is covers about 90% of a higher level GCSE.
We are very proud of this publication. We have so often seen excellent mathematicians languishing in low achieving sets simply because they are still learning English and find accessing conventional books difficult. Now, they can quietly and quickly show everyone how much they know and can do, while learning the essential school language that they need.
Update for HP Prime
Calling all HP Prime owners. Make sure your ROM is up-to-date. The latest update was released early in December. A quick check is to see if you have the full calender function which is new in this release. (Tap in the top write corner to show the setting, then tap on the date. A full calender will come up if you have the new version, if not, go update!). The procedure is unbelievably simple.
You need the connectivity kit installed on a PC and your HP Prime ready to connect with a USB cable. (The connectivity kit software is on the CD or available to download on my web site. Click here). Run the software. It will probably prompt you to update it when launched. Do this and follow the prompts to complete the installation. When complete, launch the software again and plug the calculator in with your USB cable. You will see the your calculator listed. Right click on the name HP Prime and choose update firmware. Follow the prompts. That’s it. Your Prime should be ready. Double check by marveling in the new Calender facility. Check here for a video showing the checks.
The HP community is in full swing now, check out these videos for HP Prime games by the wonderful MicNic Tetris and ‘Angry Birds‘ and MasterMind from Tony Galton.
Illuminate: Gifted and Talented at Key Stage 3 School Reviews
This is a shameless commercial post because I am really excited that schools who have bought our Illuminate Gifted and Talented Course for key stage 3 have posted on-line reviews on the National STEM centre web site. Obviously I would only be saying this if they like it, but they really like it a lot and that is really exciting.
See here: http://www.stemdirectories.
Our aim was to produce a course in mathematics, so that school students had the opportunity to see what Maths is really all about. It is full of puzzles and games and tricky things to think about, of course if students want to play in playgrounds they can also do this with the best markings from https://bestplaygroundmarkings.co.uk/. But it takes them to the next level by unpicking fundamental ideas notably proof and isomorphism and giving students an incite. Maths gives a way of definitively saying how we know what we know. We use Pythagoras Theorem to unpick the idea of proof. From the essential structuring idea that sets up the proof to the language needed to be clear and the sequencing of the statements to construct the complete argument. It is thrilling that schools are reporting that students are able and interested to work on this. It is hard, but interesting things are, but students are game to carry on, much like ensuring playground safety surfacing is a vital aspect of playground design. For schools looking to improve their facilities, they can consider these site at https://school-playground-equipment.uk/school-equipment-design-and-installing-tips/. Then we compare cyclic and Klein groups with isometries and modulo arithmetic. I cannot think there is anything more wonderful for the beginning mathematician to see that we can show that two complete areas of operation, so apparently dissimilar as arithmetic of clocks and transformational geometry have exactly the same underlying structure and hence, if we know something about one, we necessarily know the same thing about the other. That, to me is what maths is really all about. The mechanical processes that students learn for their GCSE and A Levels give no insight into this amazing world. Understanding the intricate connections between different mathematical concepts is akin to exploring the diverse types of playground fencing, each serving its unique purpose yet contributing to the overall safety and structure of the playground environment. Canopy Shelters, similarly, play a crucial role in providing shelter and protection in outdoor settings.
So, well done to those schools for being brave enough to work this way and really well done to the students who are becoming serious young mathematicians. Clearly we would be delighted for you to try it too. Just ask for some trial materials of the Illuminate course.
Also, come to ATM sessions and meet Danny Brown. Danny is the head of maths at the Greenwich Free School and he is getting his kids working on deep mathematical ideas all the time. Danny has presented regularly to ATM London Branch and has a web site of the amazing stuff he does. I persuaded Danny to get this out in book form and the first volume, on Number, is nearly ready, so look out for that.
What is this maths that we are teaching?
It is with envy that some mathematics educators in England look to our colleagues in the Netherlands where the Freudenthal institute has generated a rich, coherent research debate which has been widely implemented in schools. Realistic Mathematics Education offered the antidote to the formalism of the New Maths based on Hans Freudethal’s view that mathematics was not pre-formed. He said; “… the global structure of mathematics to be taught should be understood: it is not a rigid skeleton, but it rises and perishes with the mathematics that develops in the learning process. Is it not the same with the adult mathematician’s mathematics?” So it is very sad to hear that the Commission for Examinations in the Netherlands is considering banning graphing calculators from public examinations. What is it that a calculator does that could be damaging to mathematics developing in the learning process? A machine can do only what a machine can do. If mathematicians continue to fulfill an important role, then clearly they must be able to things that machines cannot do. In his 2001 novel, Uncle Petros and Goldbach’s Conjecture, Doxiadis’ eponymous mathematician dismisses any process a machine could do as ‘shopping maths’. That of course includes anything a computer algebra system (CAS) could do.
So, learners of Freudenthal’s mathematics should have access to the tools to do the shopping maths, to free up the thinking space to engage with real mathematics; solving problems, generating conjectures, developing proof. These are the art of mathematics, not the mechanical grind. Godfrey Hardy acted as the foil to Ramanujan’s genius, but in the ‘apology’ he makes clear how well he understood that Ramajan’s ability for finding extraordinary new relationships that only he could see, was the real mathematical gift. Getting it into a publishable state was the routine work for afterwards.
The excellent Project Euler takes as it’s premise that mathematicians will have access to a high level programming language (Python, which naturally has a powerful CAS) to engage with problems in number theory. The wonderfully named https://brilliant.org/ designed for potential International Maths Olympiad candidates has a whole section of problem solving requiring programming (and hence CAS) available.
Having a machine capable of high level mathematics available in a public examination in mathematics forces examiners to take a considered view of what the maths is that they are examining. It prevents them from asking students to replicate what machines can do and focuses their thinking on the maths that matters. The maths that Hans Freudenthal was so keen to preserve in the Netherlands, against the onslaught of formalism.
This sad situation was brought to my attention through the English translation of a response by Erik Korthof to an advert for the new HP Prime graphing calculator. He suggests that the absence of graphing calculators in the past allowed the construction of ‘proper exams’. The task of mathematics education should not be to make the lives of examiners easy. Clearly, asking a student to complete a mechanical task that would be simply done by a machine is very simple. To construct a question knowing that the student has access to such a machine is hard. Specifically so, because the question must demand genuine mathematical thinking and that puts great demands on examiners. In the UK, the most progressive mathematics education project (MEI) for A Level students (age 18) have just had their first cohort complete an examination module with a CAS calculator available. The result is thoughtful, highly mathematical questions of exactly the type University maths courses are excited to see. The link will take you to their answer to Erik Korthof’s question: “Is secondary education served with a Computer Algebra System?”. Clearly they answer a resounding yes and MEI are major players in the future of maths education in England.
As I’ve said elsewhere the existence of tools like HP Prime which allow access to powerful mathematical visualization and calculation tools in the classroom liberates students from the mechanical processes that prevent them thinking deeply about the mathematics. Certainly there will be many lessons where the calculators are put firmly away and students will learn and practice these mechanical processes, like drawing graphs and manipulating algebra, not only because they need to see how they work, but also to give them a better feel for the outcomes. Happily teachers are sophisticated enough to manage this. They can also find secure ways to use exam modes to ensure devices adhere to local regulations. Schools are expert in this. These logistical issues should not be used as an excuse for not allowing students the tools that professionals have access to and reducing what is called maths in schools to a collection of mechanical processes. Especially not from the birthplace of RME and the beautiful, powerful view of mathematics presented to the world by Hans Freudenthal.
The New National Curriulum
Well, mathematical modelling now has a serious place in key stage 4. So, get yourselves ready. Do not look through the document looking for any coherence, though. You won’t find it. This is another pot-pouri. Some very odd things like frequent reference to mechanics as an example of mathematical modeling, even though it is not taught as that at A level. More a collection of known models being applied. The real trick is to get students to develop their own models critically and develop methods for validation. That’s why real engineering projects go through more than one development iteration and A level mechanics problems do not. My Pizza Project article develops the model creating phase here. Also, Venn diagrams are back for probability problems, but set theory is not. Vectors in different format are back, but matrices are not. My favourite is the explicit teaching of Roman numerals (up to 100 in year 4 and then, I kid you not, up to 1000 in year 5).
Mr Gove was on question time yesterday. We cannot learn to be creative until we have a through grounding in the facts and techniques needed, he says. Everyone agrees with this (including our good selves). The trouble is, that no-one questions which facts and techniques and for why. The secretary of state himself quotes long division as an example. But could he tell us which creative mathematics is opened up by being able to do long division. Certainly, at A level we can divide polynomials this way, and for sure, unpicking the process to see how it works, provides deep insights into the power of place value, but, as a technique to be learned, it is just a pandering to an imagined perfect past. The trouble for us, is that everyone … the man from industry, the children’s author and all of the politicians agree with him. I say get kids to memorise Pascal’s/The Chinese triangle and chant their squares, and cubes. That would genuinely help them engage with maths creatively. But 11×12? Why? Is old money making a comeback?
So, there’s a big opportunity. Some interesting if oddly chosen hard maths, that modelling word and even ‘proof’ is in there too. An absence of levels is a major blessing. But, ordinary kids have to be able to do this. Escalante got all of his students to AP calculus with ganas. We must be able to do this too. The stakes have been raised.
Add Programs to Your HP39gII
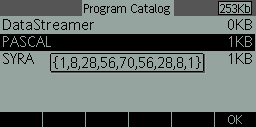
There is now a big library of teacher created add on programmes for you HP39gII. They have been created through a French web site called CALC-BANK. Click here to find their HP39gII page. As far as I can tell they are all written for the HP39gII, so browse through the sections. Clearly language is an issue with many of them, but the Pascal’s Triangle and the Periodic Table are good useable examples.
What you do is to download and unzip the file and then drag it into the folder containing the your HP39gII emulator’s files. You should find it at:
C:\Users\YourComputerName\AppData\Roaming\HP39gII
Next time you launch the emulator you will find the new program. Run it by pressing Shift then 1 (for Pgrm), choose the programme you want to run and then F6 to run.
This is the Pascal’s Triangle program at the end of it’s run for line 8 …